Pricing strategy of Our e-commerce platform
under different operational model
Abstract: We model pricing strategy under platform competition with different e-commerce’s operational models. The analysis indicates the optimal pricing strategies of the two platforms, as well as the change trends of price, and suggests four bargaining strategies based on the customer perceived value of the e-commerce platforms.
Key words: Pricing game, Operational model, E-commerce platform
1.Introduction
In the process of development of e-commerce platform, the growing of retail e-commerce always keeps the high speed on increases and the pricing model is a key question to research. Some research have already explored the pricing games of retailers and e-retailers but we notice that the price competition among e-commerce platforms get more intense, and the influence of operational models to the e-commerce platforms is become more and more obvious. In this paper, the operational models are divided into two types: the first type is that the platform set the price by and bargain with supplier and the second type is that the e-commerce provides a platform for supplier and consumers and the price of product is decided by supplier. For the same product which sells on two e-commerce platforms, the pricing model is not only related to the customer perceived value, but also influenced by the operational model. The platform of the first type should consider the wholesaling price, the competition with the second type platform and the bargaining game with the product supplier when they set the retailing price.
In this paper, we consider three keys of the pricing model: the operational model, the competition of the two platforms and the customer perceived value.
2. Model description
Here, we consider two types of operational models which are adopted by e-commerce retailer platforms with one product manufacturer. The two types of e-commerce retailer platform are denoted by m and r .
Platform m : the e-commerce provides a platform for supplier and consumers. Because that this kind of e-commerce platform does not participate in the selling activities of online sellers and each online seller have a fairly weak voice in bargaining power, so the price of product is decided by supplier;
Platform r : the platform sells product through its own channel. Relying on powerful scale advantage, this kind of e-commerce platforms purchase product from supplier set the price and bargains with supplier.
Supplier s : supplier s provides products to platform r and the online sellers of platform m . The difference is for the sellers of platform m , supplier s set the price of the product based on wholesaling and retailing, but for platform r , the price of the same product is set by the platform, based on the sales volume and wholesale price.
We can see that, the competition of e-commerce platform m and r actually translates to a competition between platform r and supplier s . In order to maximizing the profit, supplier s has to consider not only the retailing price but also the wholesaling price. The wholesaling pricing cannot be too low or else the selling of platform r will encroach on the market share of platform m ; in the meantime, it cannot be too high, otherwise the whole sales volume of the market will decrease. But for platform r , they want to use their strong bargaining power to negotiate with supplier s for a lower wholesaling price. In this way, supplier s and e-commerce platform r constitute a multi-stage game relationship which decides the online price of the two e-commerce platforms together. In this paper, we emphatically analyze the first two stages:
StageⅠ: e-commerce platform r purchases product from supplier s ; supplier s provides product to platform r and set the wholesaling price; then, platform r set price for itself and supplier s set retailing price for the online sellers of platform m . StageⅡ: based on the sales volume of stage 1, platform r bargain with supplier s ; supplier s set a new wholesaling price; then, platform r and supplier s reset the retailing price respectively.
Using the customer utility theory, we build the demand function of each platform. We choose parameter v , which is distributed in the [0, 1] interval, to denote the value
of customers buying product and αi (i = 1, 2) , which is also distributed in the [0, 1]
interval, denote the preference of the e-commerce platform m and r ,(i.e. customer perceived value). So, the utility of each e-commerce platform can be measured by
U i = αi v − pi , (i = m, r) , with pi denoting the retailing price of platform m and r .
In the meantime, we assume that the search cost of the two e-commerce platforms is 0. This assumption is realistic because that the two platforms are selling products online, the customers do not need to spend a lot to search the information of the product.
In the rest part of this paper, we use Bertrand game model to analyze the equilibrium in the two stages of this game.
3. Equilibrium analysis of stageⅠ
In this section, we analyze the equilibrium of stageⅠin this game. The same product is sold on these two e-commerce platforms, and we assume the product is sufficient and purchased from supplier at the price of the current stage whenever necessary, so based on customer utility theory, we get:


These are the demand functions of platform m and r . For e-commerce platform m , the price of product is set by supplier s , so, the payoff, which should be maximized, consists of two parts: wholesaling to platform r and retailing to customers through
platform m . But for platform
r , the whole payoff derived from its online selling.
Plugging these functions into payoff function, we get:


Among these functions, pt denote the wholesaling price for platform r , which is set
by supplier s . For convenience, in our paper, we assume the cost of production is a fixable constant C . In order to obtain maximal payoff, the price response function of platform m and r is then derived as:


These functions can be expressed by pt . After simplification, we get:


Thus, the relationship between
pm and
pr is then derived as:

Because 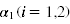
is distributed in the 0, 1] interval, so the coefficient of this
function,  , is larger than 0, which indicates that, when supplier s raises retailing price of platform m, platform r would follows the same path and vice versa.
, is larger than 0, which indicates that, when supplier s raises retailing price of platform m, platform r would follows the same path and vice versa.
Make  and
and  , we can derive three situation,
, we can derive three situation,  ,
,  and
and  . when
. when  ,
,  is less than 1 and
is less than 1 and  is less than 0, which means in this situation,
is less than 0, which means in this situation,  : when
: when  ,
,  equals to 1 and
equals to 1 and  equals to 0, which means in this situation,
equals to 0, which means in this situation,  , if platform r operates in the circumstances, the payoff of platform r will turn into 0, and platform m will sell product at wholesaling price; when
, if platform r operates in the circumstances, the payoff of platform r will turn into 0, and platform m will sell product at wholesaling price; when  ,
,  is larger than 1 and
is larger than 1 and  is larger than 0, which means in this situation,
is larger than 0, which means in this situation, 
Proposition I : In stage I, under different operational models, the retailing prices of these platforms change in the same direction. A higher consumers' sense of a e-commerce platform corresponds a higher retailing price, in the mean time, the two platforms would not adopt same price strategy, especially for platform r.
4. Equilibrium analysis of stageⅡ
In this stage, e-commerce platform r has choice to bargain with supplier s , because of strong bargaining power. Therefore, we start the analysis by deriving the retailing price and demand function of platform r . We get:


According to the above two functions, the coordinate axis of  can be divided into three intervals ;
can be divided into three intervals ;  ,
,  and
and  . We now discuss the three cases respectively.
. We now discuss the three cases respectively.
When  is distributed in the
is distributed in the  interval, in order to obtain payoff, the value of
interval, in order to obtain payoff, the value of  , in bargaining, the retailing price
, in bargaining, the retailing price  will increase and the demand of platform r will decrease. When
will increase and the demand of platform r will decrease. When  is distributed in the
is distributed in the  interval, we can get that the value of
interval, we can get that the value of  can only be
can only be  to guarantee the practical significance of the above equation, But then, the demand of platform r because 0, so, this case is false.
to guarantee the practical significance of the above equation, But then, the demand of platform r because 0, so, this case is false.
When  is distributed in the
is distributed in the  interval, the value of
interval, the value of  must in the
must in the  interval. In this case, if platform r want to cut down
interval. In this case, if platform r want to cut down  in bargaining, the retailing price
in bargaining, the retailing price  will decrease and the demand of platform r will increase. Then we derive the payoff of the two plateforms to obtain a clear bargaining strategy.
will decrease and the demand of platform r will increase. Then we derive the payoff of the two plateforms to obtain a clear bargaining strategy.


We now get the axis of symmetry of the two payoff curves. Combining with the above analysis, we compare the position of the intervals and get the discussion as follow:
For platform m , the axis of symmetry of the payoff curve is:

For platform r , the axis of symmetry of the payoff curve is:

When  is in the
is in the  interval, according to the monotonicity of these two functions, the total payoff of supplier s is monotonically increase with
interval, according to the monotonicity of these two functions, the total payoff of supplier s is monotonically increase with  , and the payoff of platform r is monotonically decrease with
, and the payoff of platform r is monotonically decrease with  , in the feasible region
, in the feasible region  . So we can get :
. So we can get :
Proposition II : When  is in
is in  interval exist
interval exist  , which makes the payoff of platform m and paltform r are equal.
, which makes the payoff of platform m and paltform r are equal.
Because the total payoff of supplier s is monotonically increasing with  in the
in the  interval, we get that, supplier s does not have the driving force to reduce the wholesaling price
interval, we get that, supplier s does not have the driving force to reduce the wholesaling price  . But for platform r, the situation is just the opposite. The payoff of platform r monotonically decrease with
. But for platform r, the situation is just the opposite. The payoff of platform r monotonically decrease with  in the feasible region
in the feasible region  , platform r has a sufficient motive to bargain with the supplier. Under the present circumstances, supplier s has two kinds of strategies.
, platform r has a sufficient motive to bargain with the supplier. Under the present circumstances, supplier s has two kinds of strategies.
When  although cutting wholesaling price will reduce its payoff, but for the sake of expanding the market share, supplier s would adopt price-off strategy and cut down the wholesaling price, and the critical value of price reduction is
although cutting wholesaling price will reduce its payoff, but for the sake of expanding the market share, supplier s would adopt price-off strategy and cut down the wholesaling price, and the critical value of price reduction is  ; When
; When  is down to
is down to  , the decreasing of
, the decreasing of  will make the payoff of supplier s is lower than platform r . So in this case, supplier s would increase the wholesaling price to bring up its payoff to the same level with platform r . Above all, we can see that, in this scenario, supplier s is the leader of this game, and can adjust the sales of platform r through the changes of wholesaling price.
will make the payoff of supplier s is lower than platform r . So in this case, supplier s would increase the wholesaling price to bring up its payoff to the same level with platform r . Above all, we can see that, in this scenario, supplier s is the leader of this game, and can adjust the sales of platform r through the changes of wholesaling price.
When  is in the
is in the  interval and monotonically decrease with
interval and monotonically decrease with  in
in  interval. The payoff of platform r is monotonically decreasing with
interval. The payoff of platform r is monotonically decreasing with  , in the feasible region
, in the feasible region  . We now can get that, in the
. We now can get that, in the  interval, both supplier s and platform r have the motive to reduce the wholesaling price. In this interval, when
interval, both supplier s and platform r have the motive to reduce the wholesaling price. In this interval, when  is decreasing, the retailing price of platform r
is decreasing, the retailing price of platform r  will decrease and the demand of platform r will increase. In the meantime, the payoff of supplier s and platform r will all increase. So in the
will decrease and the demand of platform r will increase. In the meantime, the payoff of supplier s and platform r will all increase. So in the  interval, supplier s would adopt wholesaling price-off strategy while platform r would adopt bargaining strategy to raise the payoff and the demand of product. In the
interval, supplier s would adopt wholesaling price-off strategy while platform r would adopt bargaining strategy to raise the payoff and the demand of product. In the  interval, with the decreasing of
interval, with the decreasing of  , the payoff of platform r is increasing, but the payoff of supplier s is decrease, so in this interval, although the demand of the product will increasing if
, the payoff of platform r is increasing, but the payoff of supplier s is decrease, so in this interval, although the demand of the product will increasing if  is continuously going down, supplier s would not reduce the wholesaling price, while platform r adopt bargaining strategy.
is continuously going down, supplier s would not reduce the wholesaling price, while platform r adopt bargaining strategy.
5.Final remark
In the competition of e-commerce platforms, a different operational model would lead to a different pricing strategy. In this paper, we discuss pricing strategy of the first two stages, and we get the conclusions as follow: in the first stage, these platforms would not set an identical price, and the retailing prices of these platforms change in the same direction. In the second stage, platform r will always adopt bargaining strategy in order to obtain a lower wholesaling price, but for supplier s ,
there are two Kinds of decisions for four reasons, when  is in the
is in the  interval,
interval,
supplier s is the leader of market and can influence the market through adjusting the wholesaling price. At this scenario, in the  interval, cutting wholesaling strategy will be adopted by supplier s for expanding market share; in the
interval, cutting wholesaling strategy will be adopted by supplier s for expanding market share; in the  interval, increasing wholesaling strategy will be adopted by supplier s for more payoffs. When
interval, increasing wholesaling strategy will be adopted by supplier s for more payoffs. When  is in the
is in the  interval, in the
interval, in the  interval, {bargain, increase} is the policy set of the two platform for obtaining higher payoffs; in the
interval, {bargain, increase} is the policy set of the two platform for obtaining higher payoffs; in the  interval, wholesaling price-off strategy would be adopted by supplier s to raise the payoff and the demand of product, while platform r would adopt bargaining strategy.
interval, wholesaling price-off strategy would be adopted by supplier s to raise the payoff and the demand of product, while platform r would adopt bargaining strategy.
Although we get some conclusions of the relationship of pricing strategy and operational models of e-commerce platforms, there are still something more to explore. For example, the pricing strategy under the offer level constrained conditions and more competitors. What’s more, although some of the e-commerce platforms do not have the pricing power, they provide a trading platform and charge fees, so it would be interesting to explore the pricing strategy under revenue sharing.
platform m . But for platform | r , the whole payoff derived from its online selling. |
Plugging these functions into payoff function, we get: | |
Thus, the relationship between | pm and | pr is then derived as: |
is distributed in the 0, 1] interval, so the coefficient of this |